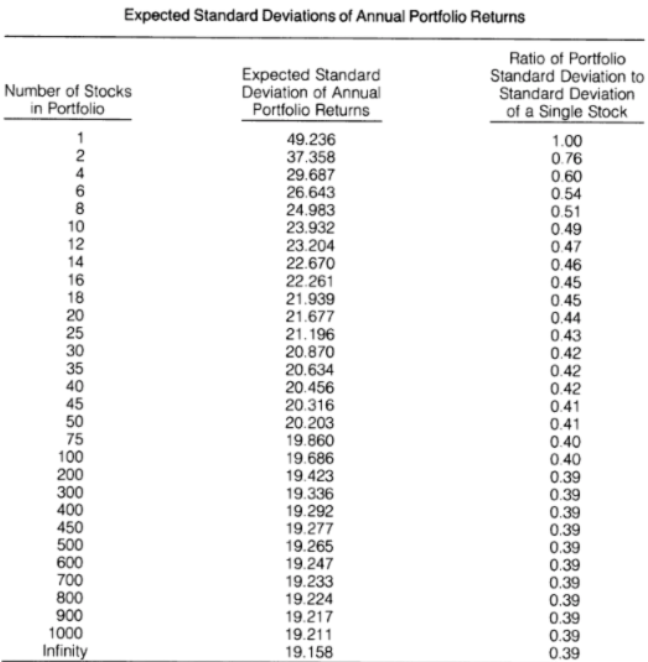
Um zielgerichtete Optimierungsprobleme formulieren zu können, müssen zunächst die Rahmenbedingungen für das Problem, welche in der Optimierung als Nebenbedingungen einfließen, definiert werden. Statman, M. beschreibt, dass ein Portfolio bei gleicher Gewichtung der Aktien im Allgemeinen ab 30 Aktien als gut diversifiziert gilt.[1] Es existieren jedoch auch Aussagen, welche ein Portfolio ab zehn Aktien als diversifiziert ansehen und argumentieren, dass darüber hinaus der marginale Diversifikationseffekt die Kosten für die
Transaktion nicht rechtfertigen.[2]
In Abbildung 5 ist zu erkennen, dass die Standardabweichung des zufälligen Portfolios im Vergleich zu einer einzelnen Aktie ab einer Anzahl von 20 Aktien jeweils mehr als 5 Aktien benötigt, um 0,01 zu sinken. Das bedeutet, dass der marginale Diversifikationseffekt ab dieser Anzahl relativ klein wird und der Aufwand für die zusätzliche Anzahl der Aktien den Nutzen gegebenenfalls nicht rechtfertigt. Zudem hat die Untersuchung von ex-post Portfolio Performances Anhaltspunkte geliefert, dass eine Limitierung der Anzahl von Wertpapieren im Portfolio robustere und praktischere Portfolien nach sich zieht.[4] Aufgrund dieser Erkenntnis und dem Versuch, aus vorausgehenden Aussagen einen Konsens zu bilden, soll ein Portfolio aus mindestens 20 Aktien optimiert werden. Somit ist die erste Nebenbedingung, dass die Gewichtung jeder Aktie im Portfolio fünf Prozent nicht übersteigen soll.
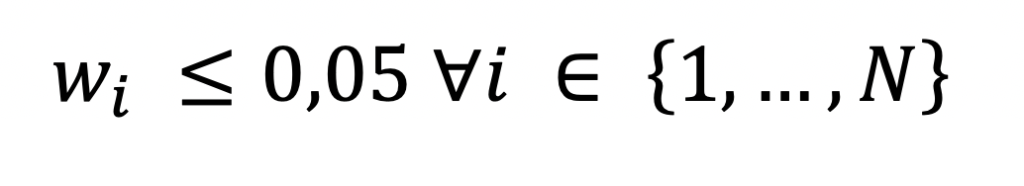
Diese Nebenbedingung ergibt im Minimalfall ein Portfolio aus 20 Aktien, welche jeweils zu fünf Prozent gewichtet sind. Um vorhergehende Bedenken zu Transaktionskosten ebenfalls in das Optimierungsproblem zu überführen, ist eine weitere Nebenbedingung, dass die Gewichtung jeder in der Masterliste enthaltenen Aktie nicht zwischen Null und ein Prozent liegt. Diese Mengenbeschränkungen dienen auch der Vereinfachung des fortlaufenden Portfoliomanagements.[5]
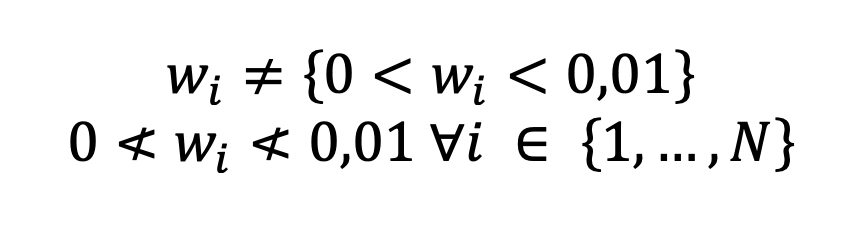
Mit dem Portfolio soll auf den Sektor Wasserstoff und nicht gegen ihn, oder einzelne darin enthaltene Unternehmen, gewettet werden. Außerdem soll das optimierte Portfolio, wie eingangs definiert, von jedem Investor umgesetzt werden können. Deshalb ist die nächste Nebenbedingung, dass Leerverkäufe verboten sind. Das bedeutet, dass jedes Gewicht im Portfolio größer oder mindestens gleich Null ist.[6]
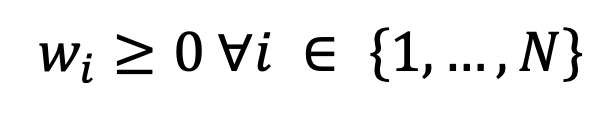
Eine weitere, mathematisch notwendige Nebenbedingung ist, dass die Summe aller Prozentualen Gewichte im Portfolio 100% ergeben muss.[7]
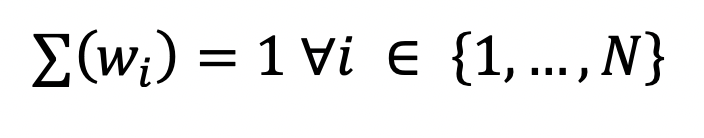
[1] Vgl. Statman, M. (1987), S. 362.
[2] Vgl. Evans, J./Archer, S. (1968), S. 767.
[3] Statman, M. (1987), S. 355.
[4] Vgl. Cesarone, F./Scozzari, A./Tardella, F. (2011), S. 25.
[5] Vgl. Cesarone, F./Scozzari, A./Tardella, F. (2011), S. 2.
[6] Vgl. Marti, K./Gröger, D. (2000), S. 3.
[7] Vgl. Gilroy, B./Mykhalskyy, V./Seiler, V. (2017), S. 14.