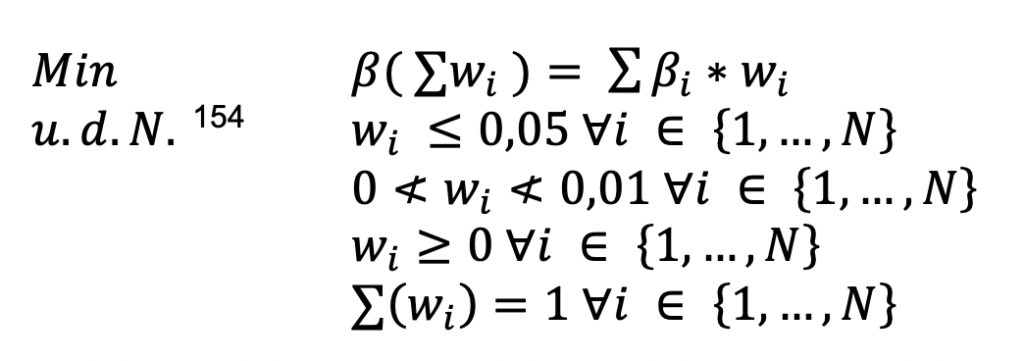Die erste Optimierung soll die Minimierung des Betas, auch als ß notiert, sein. ß beschreibt, wie sensibel jede im Portfolio enthaltene Aktie auf Marktschwankungen reagiert.[1] Da der Markt keine messbare Benchmark ist, muss eine solche festgelegt werden. Die gewählte Benchmark, welche stellvertretend für den Markt steht, ist der MSCI World Acwi All Cap Index.[2] Die Masterliste Aktien enthält Small-, Mid- und Large Caps[3], welche international verteilt sind. Der MSCI World Acwi All Cap Index enthält mehr als 14000 Aktien aus allen Unternehmensgrößen und zwischen entwickelten und aufstrebenden Märkten verteilt.[4] Aufgrund dieser Gemeinsamkeiten mit der Masterliste und einem durchschnittlichen Beta gegen das Referenzportfolio von 0,88 ist der MSCI World Acwi All Cap Index ein passender Maßstab zur Minimierung der Sensitivität des Portfolios gegen den Markt.
Das ß stellt das in Abbildung 4 dargestellte systematische Risiko dar. Wie ebenfalls in der Abbildung zu erkennen ist, stellt bei einem gut diversifizierten Portfolio das systematische Risiko den größten Teil des Gesamtrisikos dar. Deshalb ist es das Ziel einiger Investoren, diesen Teil des Risikos zu minimieren. Das Ziel der Betaminimierung ist, das Portfolio möglichst unabhängig für makroökonomische Marktschwankungen zu machen.
Das Gewicht der i-ten Aktie im Portfolio wird mit angegeben. Das ß der i-ten Aktie wird mit ßi, (i= 1,…N) angegeben. Das -Risiko wird nach folgenden Maßgaben minimiert:
Da sich das ß eines Portfolios als gewichtetes Mittel aller im Portfolio errechnet, wird unter gegebenen Nebenbedingungen das globale Minimum erreicht, wenn die 20 Aktien mit dem geringsten ß zu jeweils fünf Prozent gewichtet werden.[6] Für die Bestätigung dieser Optimierungsüberlegung wird der Excel Solver verwendet. Hierfür wurde die Problemstellung in Excel übertragen.[7]
Die zu minimierende Zielzelle mit der Formel errechnet das gewichtete Mittel aus ßi und wi, wobei alle wi der Aktien und ßi alle der Aktien sind. Als die für den Solver zu verändernden Zellen sind alle Zellen mit Aktiengewichten gewählt. Die Nebenbedingung wird durch die Formel mit Solver-Anweisung umgesetzt. Der Ausschluss kleiner Gewichte gemäß wird durch im Solver umgesetzt. Das Leerverkaufsverbot ist durch in den Solver programmiert.[8] Die Gesamtgewichtsbeschränkung ist durch einprogrammiert.[9]
Als Lösungsmethode wurde GRG-Nichtlinear gewählt und die Standardeinstellungen des Solvers wurden durch die Erhöhung der Nebenbedingungsgenauigkeit von 10-4 auf 10-7 verändert. Das Ausführen des Solvers mit der vorhergehend erläuterten Optimierungsüberlegung als Ausgangssituation ergibt die positive Rückmeldung, dass die aktuelle Lösung durch Konvergieren erreicht und alle Nebenbedingungen eingehalten wurden. Der Lösungsvorschlag des Solvers bestätigt die vorher angenommene Optimierungsüberlegung.[10]
Die Minimierung hat das Beta des in Abbildung 6 dargestellten Referenzportfolios von 0,88 auf 0,52 bei optimierter Gewichtung reduziert. Es ist eine relative Verbesserung von 69,23% erzielt worden.[11] Die maßgebliche Verbesserung lässt eine wirksame Optimierung vermuten.
Das optimierte Portfolio würde von einem Investor, welcher das Ziel der Betaminimierung verfolgt, streng gegenüber dem Referenzportfolio bevorzugt werden, da das Beta des optimierten Portfolios deutlich kleiner als das des Referenzportfolios ist. Somit ist die Optimierung hinsichtlich der Zielsetzung erfolgreich, das prognostizierte Minimum wurde als globales bestätigt.
Die gewichtete Relevanzkennziffer ist für Investoren, welche den Sektor möglichst trennscharf im Portfolio abbilden wollen, zu beachten. Die Kennziffer hat sich von 2,94% im Referenzportfolio auf 3,41% im betaoptimierten Portfolio verbessert, was einer relativen Verbesserung von 15,96% entspricht.[12] Das bedeutet, dass das betaoptimierte Portfolio den Sektor Wasserstoff besser abbildet als das Referenzportfolio.
Die jährliche Portfoliovolatilität wurde von etwa 25,78% auf rund 25,30% marginal verbessert.[13] Diese nur marginale Verbesserung kann durch den Effekt erklärt werden, dass die Diversifikation des Portfolios mit der Optimierung von 34 auf 20 Aktien verkleinert wurde. Die Einzelrisiken der Aktien fließen dann stärker in das Portfolio ein, so dass die Gesamtvolatilität trotz Betaminimierung lediglich marginal sinkt.
Eine beachtenswerte Variable ist die Kovarianz der Aktien, welche sich nach einer veränderten Gewichtung auch negativ auf die Gesamtvolatilität auswirken kann. Das nicht systematische Risiko der Aktien mit geringem Beta ist im betrachteten Datensatz höher. Die 20 Aktien mit geringstem Beta besitzen eine höhere mittlere Volatilität von 77,54% im Gegensatz zu 64,67% in der Grundgesamtheit. Ein geringeres systematischen Risiko geht im beobachteten Datensatz mit einem höheren Einzelrisiko einher. Das erschwert die Vermeidung von Risiken im Gesamten. Unter Betrachtung des Optimierungsergebnisses aus Abbildung 6 im Vergleich zum naiven Portfolio und unter Einbeziehung der Erkenntnis, dass ein Trade-off zwischen systematischem und unsystematischem Risiko besteht, ist zu erkennen, dass größere Unternehmen wegen deren breiteren Geschäftsfeldes zwar weniger Einzelrisikobehaftet sind, jedoch stärker von makroökonomischen Marktschwankungen abhängen.[14]
Eine pauschale Aussage in die andere Richtung, dass kleine Unternehmen zwar mehr Einzelrisiken tragen, dafür aber weniger Marktrisiken, lässt sich lediglich schätzungsweise treffen. Das berechnete Beta dieser Unternehmen könnte kleiner als das des Gesamtmarktes sein, weil die Sprunghaftigkeit und Zufälligkeit der Umsätze nicht der Entwicklung des Gesamtmarktes gleicht. Der Einfluss des Gesamtmarktes könnte trotzdem, wie bei größeren Unternehmen, bestehen. Bei langen Zeiträumen folgen die Beta Koeffizienten jedoch keinem Random Walk.[15] Das Beta ist wegen der teils kurzfristigen Datengrundlage mit gewisser Unsicherheit verbunden.
Die Betaoptimierung hat das Portfolio im Vergleich zum naiven Portfolio in den Bereichen Beta, Relevanz und Portfoliorendite maßgeblich verbessert, die Gesamtvolatilität konnte wegen mathematischer Effekte lediglich marginal verbessert werden. Eventuelle Abweichungen in den Betawerten sind langfristig zu vernachlässigen. Das betaoptimierte Portfolio ist in jedem der gemessenen Punkte besser als das Referenzportfolio und diesem somit streng vorzuziehen.[16]
Die Hypothese, dass ein Wasserstoffportfolio so optimiert werden kann, dass es marktüblichen Qualitätskriterien entspricht, wird durch diese Optimierungsrechnung, im Vergleich mit dem Referenzportfolio, bestätigt.
[1] Vgl. Ernst, D./Schurer, M. (2015), S. 289.
[2] Vgl. Perret-Gentil, C./Victoria-Feser, M. (2005), S. 5.
[3] Aktien mit kleiner, mittlerer und großer Marktkapitalisierung.
[4] Vgl. MSCI Inc. (Hrsg.) (2019), https://www.msci.com/documents/10199/1fbb5ec6-b5d2-4806-b873-cd9f51551701 (Stand: 27.07.2019).
[5] Unter der Nebenbedingung.
[6] Vgl. Ernst, D./Schurer, M. (2015), S. 289-291.
[7] Vgl. Ernst, D./Schurer, M. (2015), S. 299-318. Vgl. hierzu auch Anhang „Optimierung Beta, MEP, MVP.xlsx“.
[8] Vgl. Gilroy, B./Mykhalskyy, V./Seiler, V. (2017), S. 15.
[9] Vgl. Anhang „Optimierung Beta, MEP, MVP.xlsx“.
[10] Vgl. hierzu auch Anhang „Optimierung Beta, MEP, MVP.xlsx“.
[11] Vgl. Anhang „Optimierung Beta, MEP, MVP.xlsx“.
[12] Vgl. Anhang „Optimierung Beta, MEP, MVP.xlsx“.
[13] Vgl. Anhang „Optimierung Beta, MEP, MVP.xlsx“.
[14] Vgl. Shah, A./Tali, A./Farooq, Q. (2018), S. 15 f.
[15] Vgl. Klemkosky, R./Martin, J. (1975), S. 1123-1128.
[16] Vgl. Anhang „Optimierung Beta, MEP, MVP.xlsx“.