Das Minimum Varianz Portfolio, auch MVP genannt, minimiert die Varianz einer Auswahl von Aktien, welche als σ2 notiert wird. σ2 beschreibt die durchschnittliche quadrierte Abweichung der Beobachtungswerte, in diesem Fall Aktienkurse, von ihrem arithmetischen Mittel, in diesem Fall der Durchschnittskurs.[1] Die als Risikomaß verwendete Volatilität, welche als σ notiert wird, errechnet sich als Quadratwurzel der Varianz und wird allgemein mathematisch auch als Standardabweichung bezeichnet. Die beiden Risikomaße basieren auf der Risikodefinition, wonach das Risiko die Abweichung von erwarteten Renditen ist.[2]
In folgender Optimierung wird das Risikomaß Volatilität minimiert, wobei wi das Gewicht der i-ten Aktie im Portfolio ist, σi die Jahresvolatilität dieser Aktie und pij der Korrelationskoeffizient der Aktien i und j. σij ist die Kovarianz der Aktien i und j. Das Optimierungsproblem ergibt sich daraus entsprechend.[3]
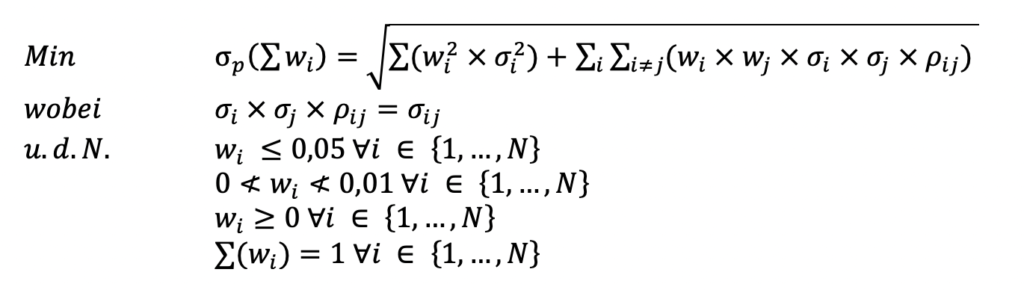
Hierbei gibt die Volatilität des Minimum-Volatilität-Portfolios an, die restlichen Variablen definieren sich wie vorhergehend eingeführt.
Zur Berechnung des Optimierungsproblems wird dieses in Excel übertragen und dem Solver die entsprechenden Anweisungen gegeben. Da sich die Berechnung hier komplexer als in vorhergegangenen Berechnungen darstellt, wird die Solver Funktion GRG Nichtlinear mit der Mehrfachstart Variante verwendet. Von 100 zufälligem Ausgangswerten und einer Grenze der Variablen zur Vereinfachung der Berechnung wird die Optimierungsrechnung durchgeführt.
Die zu minimierende Zielzelle mit der Formel errechnet die Volatilität des Portfolios aus der Varianz , der Kovarianz und dem Gewicht der Aktien . sind alle der Aktien und ist die Varianz-Kovarianz Matrix der Aktien. Als die für den Solver zu verändernden Zellen sind alle Zellen mit Aktiengewichten gewählt. Die Nebenbedingung wird durch die Formel mit Solver-Anweisung umgesetzt. Der Ausschluss kleiner Gewichte gemäß wird durch im Solver umgesetzt. Das Leerverkaufsverbot ist durch in den Solver programmiert. Die Gesamtgewichtsbeschränkung ist durch einprogrammiert. Um die Mehrfachstart Funktion effektiv verwenden zu können müssen zusätzlich nochmals die Grenzen der Variablen zwischen im Solver unter Nebenbedingungen festgelegt werden.[4]
Um mit vorhandener Rechenleistung ein optimales Ergebnis zu erzielen, wird das Optimierungsproblem mehrfach mit zufälligen Ausgangswerten ausgeführt. Zwischenergebnisse werden jeweils abgespeichert und es wird mit dem optimalsten Ergebnis weitergerechnet. Nach dem mehrmaligen Ausführen kann behauptet werden, ein globales Maximum erreicht zu haben. Das Ergebnis wird in Abbildung 8 dargestellt.
Die Optimierung des Portfolios hat die Volatilität von 25,78% auf 14,79% im Vergleich zum naiven Portfolio gesenkt. Das Beta, welches Teil des Gesamtrisikos ist, wurde von 0,88 auf 0,78 gesenkt, was erkennen lässt, dass sowohl das systematische aus auch das unsystematische Risiko gesenkt wurde. Die Relevanz ist von 2,94% auf 2,52% gesunken und die Renditeerwartung ist von 3,46% auf 1,17% gefallen. Weil mit dem optimierten Portfolio ein deutlich geringeres Risiko getragen wird, war zu erwarten, dass die Rendite fällt.[5]
Am Ergebnis der Optimierung ist gut zu erkennen, dass das Risiko eines Portfolios lediglich teilweise von den Volatilitäten der Einzelaktien abhängt. Die durchschnittliche Volatilität der Aktien im MVP beträgt 52,46% wohingegen die durchschnittliche Volatilität der Aktien, welche nicht enthalten sind, 87,05% beträgt. Gleichzeitig ist jedoch die Aktie der Powerhouse Energy Group PLC mit einer Volatilität von 103,18% enthalten und die Aktie der Firma Posco mit einer Volatilität von 32,58% nicht. Dieses Zusammenspiel von Volatilitäten, Varianzen und Kovarianzen erlaubt es mit dem Portfolio eine erwartete Volatilität von 14,79% zu erreichen, welche sogar deutlich unter der kleinsten Einzelaktienvolatilität von 20,61% liegt. Im Betrachtungszeitraum lag der Mittelwert aller Tageskurse des VIX Index, welcher die Volatilität des S&P 500 Index angibt, bei 15,10.[6] Dies bedeutet, dass der S&P 500 eine durchschnittliche Volatilität von 15,10% hat. Das hier optimierte Portfolio unterbietet das Risiko des S&P 500 Index trotz Beschränkung auf den Wasserstoffsektor.
Bei der Minimierung der Volatilität eines Portfolios stellt sich stets die Frage, ob die Minimierung dieser Kennzahl tatsächlich auch realwirtschaftliche Risiken minimiert. Zu diesem Zweck wurde das naive Portfolio in Bloomberg mit der Maßgabe, die Ausfallwahrscheinlichkeit in einem Jahr zu minimieren, unter gleichen Nebenbedingungen, optimiert.[7] Diese Optimierung, basierend auf der „Bloomberg 1 Year Default Probability“[8] ergab ein Portfolio aus 20 Aktien, welches mit dem Minium Varianz Portfolio in 16 Aktien, oder zu 80%, übereinstimmt.[9] Daraus kann geschlossen werden, dass es durch die Minimierung der Volatilität tatsächlich gelungen ist, realwirtschaftliche Risiken, wie das eines Unternehmensausfalles, maßgeblich zu verkleinern.
Aufgrund des Vergleiches mit dem Referenzportfolio, dem S&P 500 und dem Abgleich mit realwirtschaftlichen Risiken kann die Optimierungswirksamkeit und die Qualität des Minimum Volatilität Portfolios bestätigt werden. Das Portfolio entspricht den eingangs definierten marktüblichen Qualitätskriterien und bestätigt somit die Hypothese, dass ein MVP entsprechend marktüblicher Qualitätskriterien erstellt werden kann.
[1] Vgl. Ernst, D./Schurer, M. (2015), S. 88.
[2] Vgl. Bruhns, C./Meyer-Bullerdiek, F. (2013), S. 10 f.
[3] Vgl. hierzu auch Gilroy, B./Mykhalskyy, V./Seiler, V. (2017), S. 15 f.
[4] Vgl. hierzu auch Anhang „Optimierung Beta, MEP, MVP.xlsx“.
[5] Vgl. Anhang „Optimierung Beta, MEP, MVP.xlsx“.
[6] Daten von Bloomberg, Berechnung siehe Anlage „VIX Index Tageskurse.xlsx“.
[7] Optimierungsrechnung von Bloomberg ausgeführt. Parameter Vgl. Anlage „Optimierung Beta, MEP, MVP.xlsx“.
[8] Eine von Bloomberg errechnete Ausfallwahrscheinlichkeit aus Ratings und Marktdaten.
[9] Vgl. hierzu ausführlich Anlage „Optimierung Beta, MEP, MVP.xlsx“.

