Ein Investor, der nicht an die Wirksamkeit von Optimierungsrechnungen glaubt, oder eine möglichst präzise Abdeckung seines Portfolios im Wasserstoffsektor möchte, würde ähnlich zum Vorgehen beim Maximum-Ertrags-Portfolio nach diesem Optimierungsverfahren die Asset Allokation in die 20 Aktien mit der größten Relevanzkennziffer Ri vornehmen.
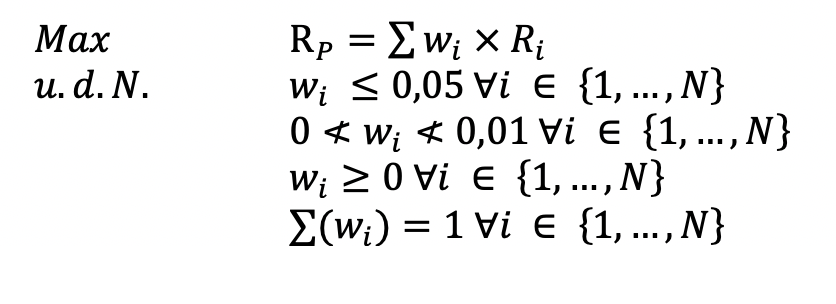
Die Ausführung des Problems, analog zum MEP, ergibt das in Abbildung 9 dargestellte Portfolio.
Die Relevanz hat sich im optimierten Portfolio von 2,94% auf 4,31% deutlich verbessert. Das Beta hat sich, von 0,88 auf 0,75, geringfügig verbessert und die Rendite hat von 3,46% auf 3,92% ebenfalls geringfügige Verbesserungen zu verzeichnen. Auffällig ist die starke Erhöhung der Volatilität von 25,78% auf 33,59% trotz Verbesserung des Betas.[1] Das bedeutet, dass die Einzelunternehmensrisiken in diesem Portfolio stark angestiegen sind. Das kann durch das hohe Risiko, welches von der Marktdurchsetzung des Wasserstoffs abhängt, erklärt werden.[2] Nach qualitativer Überprüfung des Portfolios lässt sich feststellen, dass in dem Portfolio alle wichtigen Akteure im Wasserstoffsektor vertreten sind und das Portfolio somit eine ausgezeichnete Abdeckung des Sektors bietet.
Es ist zu bemerken, dass das Portfolio die eingangs definierten marktüblichen Qualitätskriterien, also eine Volatilität von unter 30%, nicht erfüllt. Ob ein Investor bereit ist dieses zusätzliche Risiko für die bessere Abdeckung des Sektors zu tragen, ist eine individuelle Entscheidung.
Die Hypothese, dass ein betaminimiertes Portfolio, ein Maximum-Ertrags Portfolio, ein Minimum-Volatilität-Portfolio und ein Maximum-Relevanz-Portfolio im Wasserstoffsektor erstellt werden kann, wurde durch die Durchführung der Optimierungsrechnungen bestätigt.[3] Die Volatilität des Maximum-Relevanz-Portfolios entspricht jedoch nicht eingangs definierten marktüblichen Qualitätskriterien. Die Ergebnisse werden im nächsten Kapitel abschließend verglichen und in den Gesamtkontext eingeordnet.
[1] Vgl. Anhang „Optimierung Beta, MEP, MVP.xlsx“.
[2] Vgl. Albers, S. (2001), S. 81.
[3] Vgl. Anhang „Optimierung Beta, MEP, MVP.xlsx“.

